2. Portes logiques¶
En informatique, les systèmes logiques décrivent comment sont connectés les circuits électroniques des ordinateurs afin de leur permettre, d’une part, d’effectuer des calculs et de traiter des données et, d’autre part, d’utiliser leur mémoire de travail, où sont stockées les données qu’ils traitent.
Même si on a l’impression que les ordinateurs peuvent faire toutes sortes de choses, il y a un ensemble limité d’opérations de base que l’électronique d’une machine peut faire. Parmi ces quelques opérations de base, on trouve l’addition, la soustraction, la multiplication ou la division de nombres. La plupart des tâches que l’ordinateur exécute reposent sur ces quelques opérations (ainsi que sur quelques opérations dites logiques, qui vont être explicitées).
C’est assez fascinant de se dire que des tâches a priori non mathématiques, comme corriger l’orthographe ou la grammaire d’un texte automatiquement, sont réalisées avec ces opérations de base.
En parallèle à ce qui leur permet de faire des calculs, les ordinateurs disposent et utilisent de la mémoire. Il y en a au cœur des microprocesseurs, les registres, ce qu’on appelle la mémoire vive — appelée aussi RAM (Random-Access Memory). La mémoire servant au stockage de longue durée comme disques durs et autres SSD n’est pas discutée dans cette section. L’étude des systèmes logiques permet de comprendre les principes derrière la gestion de cette mémoire et de voir comment les ordinateurs peuvent y lire et écrire des données entre deux calculs.
2.1. Exemple suivi : addition de deux nombres¶
On s’intéresse à une des opérations arithmétiques les plus simples : l’addition. Comment l’ordinateur additionne-t-il deux nombres ? On va définir le cadre de travail et s’intéresser aux circuits électroniques qui vont être à même de réaliser une addition.
Que se passe-t-il pour l’addition de deux nombres entiers ? On va utiliser leur représentation binaire (avec uniquement des 1 et des 0). Pour faire simple, on va chercher à additionner simplement deux bits, disons \(A\) et \(B\), où chacun peut valoir soit 0 soit 1. Posons que la somme \(S = A + B\). En énumérant tous les cas de figure, on a :
\(A\) |
\(B\) |
\(S\) |
|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
10 |
La dernière ligne est intéressante : on sait que \(1+1=2\), mais en binaire, on sait aussi que n’existent que des 0 et des 1, et 2 s’écrit ainsi 10 (voir le chapitre représentation de l’information). Cela veut dire que, pour traiter tous les cas d’une addition de deux bits, on a besoin aussi de deux bits de sortie, et qu’un seul ne suffit pas. En explicitant chaque fois le deuxième bit de sortie, notre tableau devient :
\(A\) |
\(B\) |
\(S\) |
|---|---|---|
0 |
0 |
00 |
1 |
0 |
01 |
0 |
1 |
01 |
1 |
1 |
10 |
La question est de déterminer comment faire calculer les deux bits de la somme \(S\) à partir de \(A\) et \(B\) à un circuit électronique. Pour cela, on a besoin du concept de portes logiques. Ces portes logiques sont elles-mêmes constituées de transistors, dont on a parlé en début de chapitre.
Dans un premier temps, on détaille les portes logiques et on s’intéresse à la réalisation des circuits logiques.
Ensuite, on regarde comment, fort de cette connaissance des portes logiques, il est possible de concevoir un circuit qui effectuera l’addition en question.
Finalement, on comprendra comment un ordinateur est capable, avec un circuit logique, de stocker le résultat d’un tel calcul afin qu’il soit réutilisable plus tard.
Les opérations arithmétiques et logiques et l’accès à la mémoire ne suffisent pas à constituer un ordinateur complet. C’est dans le chapitre suivant que sera traité la problématique de l’agencement de ces sous-systèmes afin de constituer une machine capable d’exécuter une suite d’instructions, c’est à dire un programme.
2.2. Portes logiques¶
Les circuits électroniques qui composent un ordinateur sont constitués de composants électroniques comme des résistances, des condensateurs, des transistors, etc., qui déterminent où va passer le courant électrique et sur quelles parties du circuit règnera quelle tension.
Quand on parle de portes et de circuits logiques, on simplifie tout cela. On considèrera simplement qu’un segment de circuit électronique où la tension est nulle (0 volt) représente la valeur binaire 0, alors qu’une tension non nulle (par exemple, 3 volts) représente la valeur binaire 1. Ainsi, pour véhiculer deux bits comme \(A\) et \(B\) dans un circuit, on a besoin de deux «fils».
Les portes logiques sont des composants électroniques (eux-mêmes constitués en général de transistors et résistances) qui ont une ou plusieurs entrées et qui combinent ces entrées pour produire une sortie donnée. La manière dont la sortie est calculée dépend du type de la porte. On se propose à présent d’étudier en détails l’ensemble de ces portes.
2.3. Porte ET¶
Une de ces portes est la porte ET. Elle a deux entrées, qu’on appellera \(X\) et \(Y\), et une sortie \(Z\). \(Z\) sera 1 si et seulement si aussi bien \(X\) que \(Y\) valent 1. D’où son nom: il faut que \(X\) et \(Y\) soient à 1 pour obtenir un 1 sur la sortie.
En énumérant les quatre possibilités pour les entrées, on peut écrire ce qu’on appelle table de vérité pour la porte ET :
\(X\) |
\(Y\) |
\(Z\) |
|---|---|---|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
On peut dessiner des diagrammes avec des portes logiques. Ce ne sont pas des diagrammes électroniques, ils cachent une partie de la complexité réelle des circuits. Dans un tel diagramme logique, la porte ET est représentée ainsi :
Sur ce schéma logique, les entrées sont à gauche, la sortie à droite et la porte est connectée au milieu. Les circuits sont représentés en noir s’ils véhiculent un «0» et avec une couleur s’ils véhiculent un «1».
Cliquez sur l’entrée
Pour aller plus loin
Comment une porte ET est-elle elle-même construite ? Cela a déjà été mentionné : avec d’autres composants électroniques plus simples. En simplifiant un peu, on peut considérer qu’une porte ET est constituée de deux transistors :
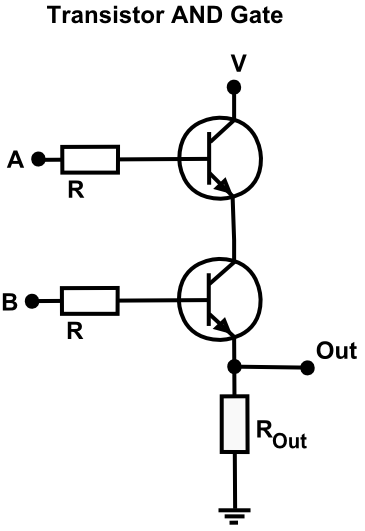
Construction d’une porte logique ET à partir de deux transistors (et de résistances).¶
Ici, les deux transistors sont les composants symbolisés par un cercle. Rappelons qu’ils laissent passer du courant de haut en bas lorsqu’ils détectent un courant sur l’entrée qui vient de la droite. Ici, si V représente une tension continue de, disons, 5 volts, on aura donc une tension similaire sur la sortie Out que si à la fois A et B, qui sont ici les entrées du circuit, sont «actives» — donc lorsque les deux transistors sont «ouverts». Sinon, on aura une tension de 0 volts sur la sortie Out.
2.4. Porte OU¶
Pour que la sortie de la porte OU vaille 1, il suffit que l’une des deux entrées \(X\) ou \(Y\) vaille 1.
Voici sa table de vérité:
\(X\) |
\(Y\) |
\(Z\) |
|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
On notera que le OU logique est un peu différent du «ou» que l’on utilise en général à l’oral : on voit à la dernière ligne de la table de vérité que la sortie \(Z\) vaut également 1 si les deux entrées \(X\) et \(Y\) valent 1. À l’oral, le «ou» est en général interprété comme exclusif: si l’on propose à un ami un bonbon ou une glace, on exclut la possibilité qu’il choisisse les deux. Ce n’est pas le cas pour le OU logique.
Essayez la porte OU :
2.5. Porte NON¶
Cette porte est plus simple : elle n’a qu’une entrée, et sa sortie se contente d’inverser la valeur en entrée. On l’appelle d’ailleurs aussi un inverseur.
Voici sa table de vérité :
\(X\) |
\(Z\) |
|---|---|
0 |
1 |
1 |
0 |
Essayez l’inverseur :
Ensemble, les portes ET, OU et NON représentent les relations logiques de la conjonction, la disjonction et la négation. Même si on ne les appelle pas ainsi, on utilise tous les jours des relations logiques de conjonction, de disjonction et de négation.
La conjonction est ainsi l’«intersection logique» de deux propositions. Si on dit «je vais à la piscine s’il fait beau ET que mes amis m’accompagnent», on utilise la conjonction.
Au contraire, si on dit «je vais à la piscine s’il fait beau OU que mes amis m’accompagnent», on utilise la disjonction, qui est comme une sorte de «somme logique» de deux propositions (même si, comme noté plus haut, le «ou», dans le langage courant, est généralement exclusif, contrairement au OU logique, qui est inclusif).
La négation est encore plus évidente, puisque la proposition «je ne vais pas à la piscine» est simplement la négation, ou l’inverse, de la proposition «je vais à la piscine».
Ressource complémentaire
Une application pour s’exercer à l’interprétation des conjonctions, disjonctions et négations logiques: The Boolean Game
2.6. Combinaisons de portes¶
Les portes peuvent être connectées les unes aux autres. Voici par exemple un diagramme logique réalisant la fonction appelée OU-X, qui est un «ou exclusif» et dont la sortie
Ce circuit contient une porte OU, deux portes ET et un inverseur, tous interconnectés.
Ce diagramme n’est pas forcément facile à lire — discutons d’abord comment l’interpréter avec papier et crayon pour vérifier s’il effectue bien un OU-X.
Analyse d’un circuit¶
Pour analyser un circuit logique comme celui présenté ci-dessus, on cherchera à établir sa table de vérité. En l’occurrence, comme pour les portes précédentes, ce circuit a deux entrées: si chaque entrée peut valoir 1 ou 0, on a en tout, de nouveau, quatre configurations possibles à examiner dans le but de remplir la dernière colonne :
\(X\) |
\(Y\) |
\(Z\) |
|---|---|---|
0 |
0 |
\(???\) |
1 |
0 |
\(???\) |
0 |
1 |
\(???\) |
1 |
1 |
\(???\) |
Pour remplir chaque ligne, on va changer les entrées selon les valeurs de \(X\) et \(Y\) et observer l’effet des portes et ainsi voir comment le circuit se comporte. Prenons \(X=Y=0\): c’est le cas représenté par le diagramme fixe ci-dessous. Rappelons qu’un segment noir véhicule un «0», alors qu’un segment coloré véhicule un «1».
Le résultat intermédiaire des deux portes de gauche sera 0. L’inverseur transforme en 1 la sortie de la porte ET, mais la porte finale, qui est aussi une porte ET, n’obtient qu’un seul 1 en entrée et donc livre une sortie de 0.
Le cas est différent si l’une des deux entrées vaut 1. Voici deux diagrammes fixes, une fois pour \(X=1, Y=0\) et une fois pour \(Y=1, X=0\) :
Ici, dans les deux cas, la porte OU, en haut, livrera un 1, dont a besoin la porte ET finale de droite pour donner une sortie de 1. La porte ET du bas, elle, continue de livrer un 0.
Mais dans le cas \(X = Y = 1\), représenté ici, la situation est différente :
La porte ET du bas livre un 1, qui est inversé en 0 avant d’atteindre la porte finale, qui ne peut dès lors elle-même que livrer un 0 comme sortie.
La table de vérité complétée de ce circuit est ainsi :
\(X\) |
\(Y\) |
\(Z\) |
|---|---|---|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
Cette fonction s’appelle «ou exclusif», car pour avoir un 1 de sortie, elle exclut le cas où les deux entrées sont 1 en même temps. Elle est souvent utilisée, au point qu’on la représente en fait dans les diagrammes simplement par le dessin de cette porte, appelée OU-X, comme simplification du diagramme ci-dessus :
Exercice 1 : vérification d’une porte
Vérifiez que la porte OU-X se comporte bien comme le circuit ci-dessous réalisé avec des portes ET, OU et NON.
Création d’un circuit¶
On s’intéresse à présent à la création de ce diagramme réalisant un OU-X avec les portes à disposition à partir de sa table de vérité. Plusieurs approches sont possibles, et on constatera que, suivant l’approche, on aurait très bien pu créer un circuit logique différent réalisant la même fonction.
Approche ad hoc
On se dit donc, selon la table de vérité, que la sortie de notre circuit «ou exclusif» doit être 1, donc l’une ou l’autre des entrées \(X\) ou \(Y\) est à 1, mais pas les deux. On peut ainsi commencer par insérer une porte OU dans le diagramme, qui fait une partie du travail. Mais il faut modifier sa sortie, pour ne pas avoir la valeur 1 lorsque les deux entrées sont à 1 : cela contredirait la quatrième ligne de la table de vérité. Comment effectuer cela ? En connectant la sortie de cette porte OU à une nouvelle porte ET à droite (dont on n’a pas encore déterminé la seconde entrée).
Pourquoi rajouter une porte ET ? On utilise ici le fait que connecter une porte ET à un signal peut restreindre les conditions sous lesquelles la nouvelle sortie \(Z\) sera 1 (alors qu’au contraire, on aurait pu étendre ces conditions si on avait connecté une nouvelle porte OU). Comme si, pour être d’accord de finalement livrer 1 sur la sortie, la porte ET voulait la «confirmation» d’un autre signal avant de livrer 1…
À ce moment, on a ce diagramme partiel, qui peut être lu comme : «la sortie \(Z\) sera 1 lorsque ces deux conditions sont vraies en même temps: (1) le OU de \(X\) et \(Y\) vaut 1, et (2) quelque chose qui reste ici à définir, qui sera connecté à la seconde entrée de la porte ET».
Ce qui reste à définir en complétant avant la porte ET, c’est l’exclusion du cas où \(X\) et \(Y\) valent les deux 1, de manière à ce que la condition (2) puisse être lue comme «\(X\) et \(Y\) ne sont pas en même temps les deux à 1». Avec une porte ET connectée directement aux deux entrées
La lecture finale du circuit est donc «la sortie \(Z\) sera 1 lorsque ces deux conditions sont vraies en même temps (selon la porte ET de droite) : (1) le OU de
Exercice 2 : analyse d’un circuit
Ceci est le même circuit que ci-dessus, mais sans la porte ET finale. À la place, on a inséré deux sorties intermédiaires, \(I\) et \(J\), qui sont les deux signaux qui allaient précédemment à la porte ET :
Combien de lignes a une table de vérité pour \(I\) et \(J\) en fonction des deux entrées \(X\) et \(Y\) ? Écrivez cette table de vérité.
Quelle différence y a-t-il entre \(J\) et ce qu’on obtient en connectant directement une porte ET aux entrées \(X\) et \(Y\) : quel élément du schéma réalise cette différence ?
Dans votre table de vérité, ajoutez une colonne et remplissez-là : elle doit représenter une nouvelle sortie \(K\), qui serait produite si on connectait une porte OU en lui donnant \(I\) et \(J\) comme entrées, comme montré ci-dessous. Le schéma représente ici le circuit dans un état indéterminé, mais les types des portes ont été ajoutés pour vous aider. La sortie \(K\) est-elle ici toujours la même que la sortie \(Z\) plus haut ? Quelles sont les éventuelles différences ? Finalement, la sortie \(K\) a-t-elle un intérêt ?
Approche systématique
Il est parfois difficile d’avoir l’«intuition» nécessaire pour suivre une telle approche ad hoc. Voici donc une autre technique, illustrée avec le même exemple.
La table de vérité montre qu’il y a deux lignes où la sortie doit valoir 1 : (a) la ligne où \(X=1\) et \(Y=0\), et (b) la ligne où \(X=0\) et \(Y=1\). Si l’on pouvait créer un premier sous-circuit qui livre un 1 lorsque qu’on se trouve dans la circonstance (a) et un autre sous-circuit qui livre un 1 lorsqu’on se trouve dans la circonstance (b), on pourrait ensuite les combiner avec une porte OU et ainsi construire notre sortie \(Z\) ainsi :
Ici, les deux sous-circuits notés avec «?» et encadrés donc encore à définir — potentiellement avec plus d’une seule porte. Essayons de les créer.
Disons que le sous-circuit du haut correspond à la deuxième ligne de la table de vérité, le cas de figure (a). Pour cette ligne, nous voulons un 1 de sortie lorsque \(X=1\) et \(Y=0\). En lisant littéralement cette dernière phrase, on y détecte un ET de deux conditions qui doivent être remplies: \(X=1\) et \(Y=0\). Mais ajouter une porte ET directement avec les signaux \(X\) et \(Y\) ne fera pas l’affaire, parce que cela livrerait un 1 lors que les deux entrées \(X\) et \(Y\) sont à 1. La solution ici, c’est d’inverser
On avance ainsi à ceci :
Pour la condition (b), qui correspond à la troisième ligne de la table de vérité, un raisonnement similaire s’applique. À la place d’inverser \(Y\), on inversera cette fois
Voici le circuit final ainsi réalisé :
(Ce schéma ne peut être simulé que dans l’indice de l’exercice suivant.)
Ce que cette approche systématique apprend, c’est qu’un circuit peut toujours être pensé comme un OU de toutes les conditions sous lesquelles la sortie doit être à 1. Ces conditions sont elles-mêmes réalisables avec les entrées du circuit avec des portes ET et des inverseurs directement connectés aux entrées.
On fait également les constats suivants :
plusieurs circuits logiques différents peuvent réaliser la même fonction de sortie,
l’approche systématique décrite ici ne livre pas forcément le circuit le plus compact: on a obtenu un circuit avec cinq portes pour réaliser un OU-X alors que l’approche ad hoc a conduit à la construction d’un circuit à quatre portes.
Exercice 3 : analyse d’un circuit
En annotant le schéma logique avec les quatre cas de figure possibles pour les entrées \(X\) et \(Y\), faites l’analyse du circuit OU-X ci-dessus construit avec l’approche systématique et montrez que la table de vérité ainsi reconstituée est la même que celle de la porte OU-X.
Indice
Exercice 4 : porte cachée
Quelle est la porte cachée de ce circuit ?
Corrigé
C’est une porte OU.
Exercice 5 : circuit défectueux
Analysez ce circuit. De quel type de portes est-il constitué ? Fonctionne-t-il correctement ? Déterminez ce qui pose problème. Dites ce que fait ce circuit une fois corrigé et écrivez sa table de vérité.
Indice
Voici le circuit corrigé (il a la même apparence que le circuit de la question, mais toutes les portes fonctionnent ici correctement).
Corrigé
Ce circuit est constitué de deux portes ET. Mais la porte ET de droite semble poser problème, parce qu’elle se comporte comme une porte OU ! Le circuit montré dans l’indice se comporte correctement.
Ce circuit, une fois corrigé, implémente en fait un ET à trois entrée \(X\), \(Y\) et \(W\), où la sortie \(Z\) ne vaut 1 que si les trois entrées valent 1. Sa table de vérité, à huit lignes dues aux trois entrées, est ainsi la suivante :
\(X\) |
\(Y\) |
\(W\) |
\(Z\) |
|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Exercice 6 : conception d’un circuit
Écrivez la table de vérité de ce circuit, dont une partie est masquée :
Corrigé
\(X\) |
\(Y\) |
\(Z\) |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
Réalisez ensuite un circuit logique avec les mêmes deux entrées \(X\) et \(Y\) et la même sortie \(Z\) qui implémente cette table de vérité. On peut utiliser des portes ET et OU et des inverseurs. Glissez les portes depuis la gauche pour en ajouter, et glissez entre les connecteurs rond pour les connecter.
Indice 1
On peut lire cette fonction comme «\(Z\) vaut 1 lorsque \(X\) et \(Y\) sont les deux à 0 (la première ligne de la table de vérité) ou lorsque \(X\) est à 1 (les deux dernières lignes)».
Indice 2
\(Z\) est donc le OU de \(X\) et du ET de l’inverse de \(X\) et de \(Y\).
Corrigé
Il y plusieurs solutions possibles. Celle qui correspond aux indices est la suivante:
Une autre solution est la suivante, où on se dit qu’on construit d’abord une partie du circuit qui identifie le cas où \(X=0\) et \(Y=1\), et on l’inverse pour correspondre à la table de vérité.
Voici un circuit plus simple, qui fait la même chose mais qui est plus difficile à concevoir d’emblée :
En fait, il existe même une porte spéciale qui réalise exactement la fonction correspondant à la table de vérité, la porte IMPLIQUE :