5. Solutions heuristiques¶
Matière à réfléchir VI
Vous avez décidé de faire le tour du monde. Choisissez cinq pays que vous souhaitez visiter et placez-les sur une carte. Essayez de trouver le meilleur itinéraire pour visiter ces cinq pays. Quels critères avez-vous pris en compte pour décider du meilleur itinéraire, c’est-à-dire un itinéraire qui minimise la distance parcourue ?
Vous avez décidé de visiter dix pays. Est-ce qu’il est aussi facile de trouver un itinéraire optimal ?
Imaginez que vous souhaitez visiter plus de la moitié des pays du monde, environ cent. Combien y a-t‑il d’itinéraires possibles ? Comment s’appelle ce nombre ?
Si le calcul d’un itinéraire prenait 1 milliseconde, combien de temps faudrait-il pour trouver la meilleure solution en énumérant toutes les solutions possibles ? Pour comparaison, le nombre d’atomes dans l’univers est d’ordre 1080.
Complexité exponentielle¶
Il existe des problèmes difficiles à résoudre. Nous allons étudier un problème qui s’appelle le problème du sac à dos. Prenons un sac à dos et une multitude d’objets qui ont chacun un poids et une valeur. Notre objectif est de choisir quels objets mettre dans le sac à dos pour maximiser la valeur totale des objets contenus dans le sac, mais sans dépasser la capacité du sac à dos (le poids maximal qu’il peut contenir).
Comment procéderiez-vous pour résoudre ce problème ? Prenez le temps d’imaginer un algorithme qui puisse résoudre ce problème ? Est-ce que votre algorithme donne toujours la meilleure solution ?
L’algorithme le plus simple pour résoudre ce problème consiste à énumérer les différentes possibilités de contenus du sac, l’une après l’autre, et de calculer pour chacune la valeur totale. A la fin de l’algorithme il suffit de sélectionner la combinaison qui à la valeur totale la plus grande. Pour 10 objets, combien de combinaisons possibles existe-t-il ? Pour chaque objet, on a deux choix possibles : le mettre dans le sac ou de ne pas le mettre dans le sac. To put or not to put, that is the question. Ces deux possibilités existent pour chacun des 10 objets. Donc le nombre de combinaisons possibles est le suivant :
2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 = 210
Pour n objets, le nombre de solutions possibles est de 2n. Si on a 2 objets, il y a 4 combinaisons différentes d’objets dans le sac. Pour 3 objets, le nombre de combinaisons est 8. Pour 5 objets, nous avons 32 possibilités à explorer. Pour 10 objets, ce nombre monte à 1024. Pour 100 objets, ce nombre devient prohibitif et vaut 1030. Si on doit résoudre ce problème avec 270 objets sous la main, le nombre de combinaisons possibles dépasse le nombre d’atomes dans l’univers (1080). Si le calcul d’une combinaison prenait une microseconde, il nous faudrait pour résoudre ce problème bien plus que le temps de l’univers. Cela va de soi, nous n’avons pas ce temps à disposition.
L’ordre de complexité de type 2n est un ordre de complexité exponentielle. Cela vaut aussi pour d’autres constantes que 2, par exemple 10n ou 1.1n. Lorsqu’un algorithme est d’ordre de complexité exponentielle ou O(an), cela veut dire que le temps nécessaire pour résoudre le problème croît exponentiellement en fonction de la taille des données n (voir figure ci-dessous) et ne peut être résolu dans un temps raisonnable (pour des données à partir d’une certaine taille).
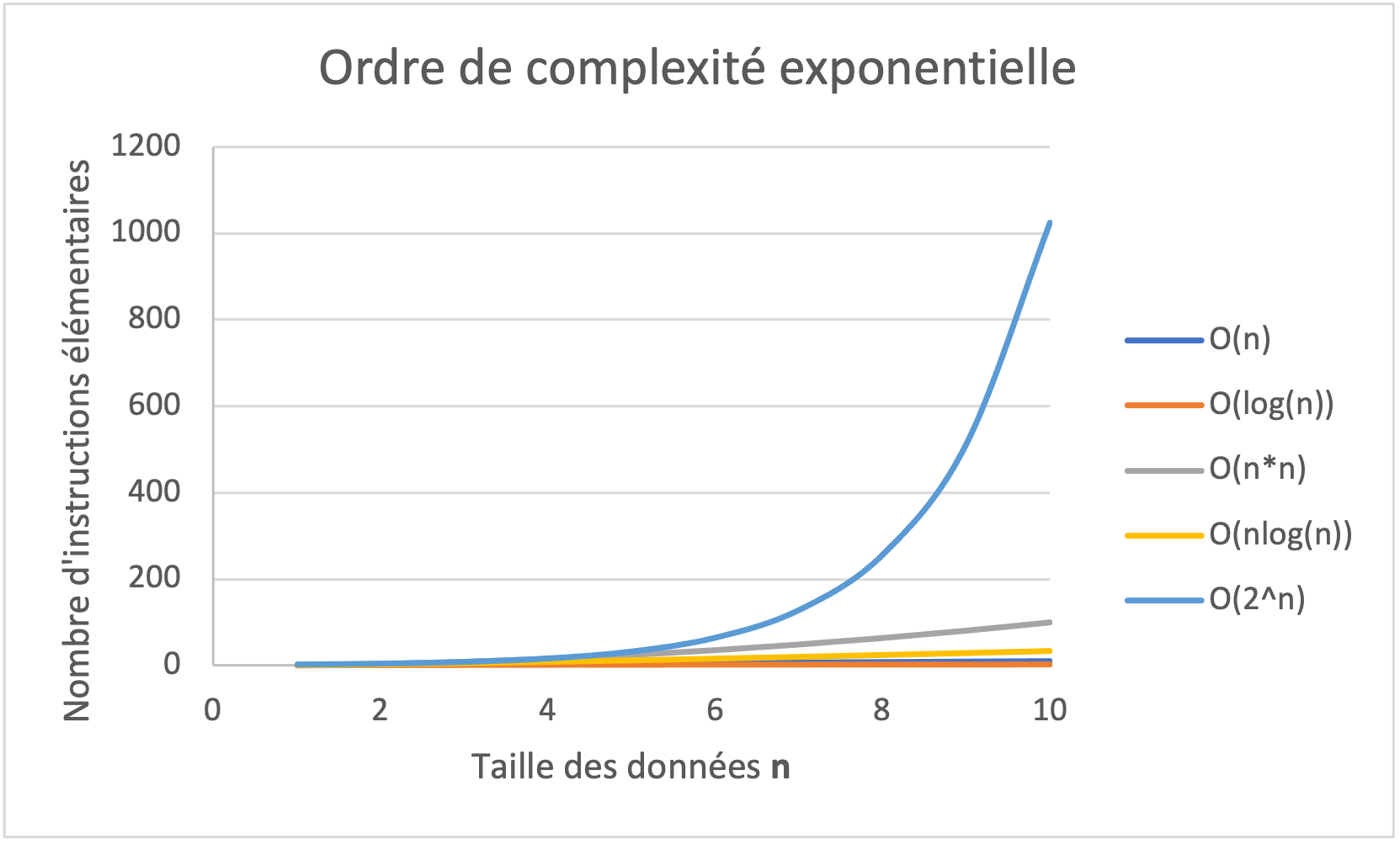
Comparaison de l’ordre de complexité exponentielle avec les ordres de complexité vus jusqu’ici. Dans un ordre de complexité exponentielle, le nombre d’instructions élémentaires grandit très rapidement avec la taille des données, et l’algorithme est de plus en plus lent.¶
Lorsqu’il est trop difficile de trouver une solution exacte à un problème, il ne faut pas s’avouer vaincu·e. Dans ce cas on peut tout de même rechercher une solution imparfaite, mais qui se rapproche autant que possible de la solution optimale. On appelle cela une solution heuristique.
Une solution heuristique pour le problème du sac à dos serait la solution suivante : ajouter d’abord les objets avec la plus grande valeur, jusqu’à ce que le sac soit plein. Intuitivement, on comprend pourquoi cette solution est facile à trouver et pourquoi elle s’approche de la solution optimale. Mais en aucun cas, on ne peut garantir que l’on va obtenir la meilleure solution. Dans certains cas même, cette solution sera très mauvaise. On appelle ce type d’algorithmes, c’est-à-dire un algorithme qui trouve une solution localement optimale (qui choisit le meilleur objet en apparence, sans se préoccuper des différentes combinaisons), un algorithme glouton.
Il n’y a pas que des heuristiques gloutonnes. Il existe d’autres types d’heuristiques, plus lentes, mais qui permettent de s’approcher davantage de la solution optimale. Il existe des stratégies de résolution statistiques, génétiques, neuronales, parmi d’autres. La majorité des problèmes que l’on tente de résoudre aujourd’hui sont difficiles et les solutions de leurs algorithmes ne donnent pas la meilleure solution.
Exercice 1 : univers et sac à dos ✏️📒
L’âge estimé de l’univers est de 14 milliards d’années. Si le calcul d’une combinaison d’objets dans le problème du sac à dos prenait une microseconde, pour quel nombre d’objets est-il possible de trouver une solution exacte sans dépasser l’âge de l’univers ?
Solution
Exercice 2 : parcours de tableaux ✏️📒
Quelle est la complexité d’un algorithme qui doit parcourir un tableau deux fois, pour chacun de ses éléments (au lieu d’une fois comme pour le tri par sélection) ?
Solution
Pour aller plus loin
Voici un problème à un million de dollars, un parmi les sept problèmes mathématiques du prix du millénaire qui rapporteront de l’argent à celui ou celle qui les résoudra.
On appelle la classe des algorithmes qui sont faciles à résoudre la classe des problèmes P. Ces algorithmes peuvent être résolus en un temps polynomial en fonction de la taille des données n ou log(na).
Il existe aussi une classe de problèmes difficiles (d’ordre de complexité exponentielle), mais pour lesquels il est facile de vérifier si une solution proposée permet de résoudre le problème. Cette classe de problèmes s’appelle NP ou « non déterministe polynomial ».
On souhaite savoir si les problèmes NP peuvent être résolus en un temps P, ou en d’autres termes : est-ce que P = NP ?
S’il s’avérait que c’est bien le cas (ce qui est tout de même peu probable), beaucoup de problèmes difficiles à résoudre deviendraient d’un seul coup plus faciles à résoudre, comme le problème de repliement des protéines en biologie pour trouver de nouveaux médicaments. Cela pourrait également signifier la fin de la cryptographie telle qu’elle existe actuellement.